Representation Lerning on Graphs: Methods and Applications

Link to paper

Link to slides

Node Embeddings

Encoder-Decoder Perspective

We want to encode nodes $v_i$ as low-dimensional vectors $\textbf{z}_i$ that summarize their graph position and the structure of their local graph neighborhood. The embeddings should then contain all information necessary for downstream machine learning tasks.

The decoder is a function that accepts a set of node embeddings and decodes user-specified graph statistics like whether a link exists. The vast majority of works use a basic pairwise decoder: $\text{DEC}:\mathbb{R}^{d}\times\mathbb{R}^{d}\rightarrow\mathbb{R}^{+}$, which quantifies the proximity of two nodes in the original graph.

Assume $s_{\mathcal{G}}$ is a ground truth graph-based proximity measure between a pair of nodes. Example measures include whether a link exists or the probability of $v_i$ and $v_j$ co-occurring on a fixed-length random walk over $\mathcal{G}$. One common thing is to reconstruct the proximity measure with the decoder by optimizing

$$\begin{equation} \mathcal{L}=\sum_{(v_i,v_j)\in \mathcal{D}}\ell(\text{DEC}(\textbf{z}_i,\textbf{z}_{j}), s_{\mathcal{G}}(v_i,v_j)) \end{equation}$$

for some loss function $\ell$.

Direct Encoding

For direct encoding, the encoder is defined as

$$\begin{equation} \text{ENC}(v_i)=\textbf{Z}\textbf{v}_i, \end{equation}$$

where $\textbf{Z}\in\mathbb{R}^{d\times|V|}$ are the parameters optimized directly and $v_i$ is a one-hot indicator vector indicating the column of $\textbf{Z}$ corresponding to node $v_i$.

Matrix Factorization-based Approaches

Laplacian eigenmaps. The decoder is defined to be

$$\begin{equation} \text{DEC}(\textbf{z}_i,\textbf{z}_j) = ||z_i-z_j||_{2}^{2} \end{equation}$$

and the loss function weights pairs of nodes according to their proximity in the graph:

$$\begin{equation} \mathcal{L} = \sum_{(v_i,v_j)\in \mathcal{D}}\text{DEC}(\textbf{z}_i,\textbf{z}_j)s_{\mathcal{G}}(v_i,v_j). \end{equation}$$

Inner-product methods.

$$\begin{equation} \text{DEC}(\textbf{z}_i,\textbf{z}_{j}) \propto \textbf{z}_{i}^{T}\textbf{z}_j \end{equation}$$

The Graph Factorization algorithm, GraRep, and HOPE all fall firmly within this class. All three methods use an inner-product decoder and a mean-squared-error loss between $\text{DEC}(\textbf{z}_i,\textbf{z}_j)$ and $s_{\mathcal{G}}(v_i,v_j)$, and they differ primarily in the definition of $s_\mathcal{G}(v_i,v_j)$:

• Graph Factorization: $s_{\mathcal{G}}(v_i,v_j):=A_{i,j}$

• GraRep: $s_{\mathcal{G}}(v_i,v_j):=A_{i,j}^{2}$

• HOPE: general proximity measure

The various proximity measure trades off between different orders of proximity. When the order becomes large, this corresponds to measuring neighborhood overlapping.

When averaging over all nodes, they optimize loss functions (roughly) of the form:

$$\begin{equation} \mathcal{L}\approx ||\mathbf{Z}^{T}\mathbf{Z}-\mathbf{S}||_{2}^{2}, \end{equation}$$

where $\mathbf{S}_{i,j}=s_{\mathcal{G}}(v_i,v_j)$

Random Walk Approaches

Many recent successful methods that also belong to the class of direct encoding approaches learn the node embeddings based on random walk statistics. Basically they optimize the node embeddings so that nodes have similar embeddings if they tend to co-occur on short random walks over the graph. These methods employ a flexible, stochastic measure of graph proximity.

DeepWalk and node2vec:

$$\begin{align} \text{DEC}(\textbf{z}_i,\textbf{z}_j) &:= \frac{e^{\textbf{z}_{i}^{T}\textbf{z}_j}}{\sum_{v_{k}\in\mathcal{V}}e^{\textbf{z}_{i}^{T}\textbf{z}_{k}}}\\ &\approx p_{\mathcal{G}, T}(v_j|v_i), \end{align}$$

where $p_{\mathcal{G},T}(v_j|v_i)$ is the probability of visiting $v_j$ on a length-$T$ random walk starting at $v_i$, with $T\in\{2,\cdots, 10\}$. Note $p_{\mathcal{G}, T}$ is not symmetric.

More formally, these approaches attempt to minimizing the following cross-entropy loss:

$$\begin{equation} \mathcal{L}=\sum_{(v_i,v_j)\in\mathcal{D}}-\log(\text{DEC}(\textbf{z}_i,\textbf{z}_j)), \end{equation}$$

where $v_j\sim p_{\mathcal{G},T}(v_j|v_i)$. However, naively evaluating this loss is prohibitive expensive with complexity $O(|\mathcal{D}||\mathcal{V}|)$, with $|\mathcal{V}|$ comes from denominator for $\text{DEC}(\cdot,\cdot)$. Thus DeepWalk and node2vec approximates the loss in different ways. DeepWalk employs a ''hierarchical softmax'' technique to compute the normalizing factor, using a binary-tree structure to accelerate the computation.

Below is an example of hierarchical softmax:

In contrast, node2vec approximates the normalizing factor using a set of random ''negative samples'' rather than the full vertex set.

The key distinction between node2vec and DeepWalk is that node2vec allows for a flexible definition of random walks, whereas DeepWalk uses simple unbiased random walks over the graph. In particular, node2vec introduces two random walk hyperparameters, $p$ and $q$, that bias the random walk.

$p$ controls the likelihood of immediately revisiting a node in the walk. Setting it to a high value ensures that we are less likely to sample an already visited node in the following two steps. This strategy encourages moderate exploration and avoids $2$-hop redundancy in sampling. On the other hand, if $p$ is low, it would keep the walk "local" to the starting node $v$.

$q$ controls the likelihood of visiting one-hop neighborhood. If $q > 1$, the random walk is more inclined to visit nodes close to the starting node. If $q < 1$, the random walk is more inclined to visit nodes which are further away from the starting node.

By controlling $p$ and $q$, node2vec is able to smoothly interpolate between walks that are more akin to BFS or DFS and trade off between learning embeddings that emphasize community structures or embeddings that emphasize local structural roles.

Large-scale information network embeddings (LINE) This work in fact does not use random walk, but is frequently compared with the two work we mentioned above. This work combines two encoder-decoder objectives that optimize "first-order" and "second-order" graph proximity. The first-order objective uses a decoder based on the sigmoid function

$$\begin{equation} \text{DEC}(\textbf{z}_i,\textbf{z}_j)=\frac{1}{1+e^{-\textbf{z}_{i}^{T}\textbf{z}_j}} \end{equation}$$

and $s_{\mathcal{G}}(v_i,v_j)=\textbf{A}_{i,j}$ with $A$ normalized. The second-order encoder-decoder objective is similar but considers two-hop adjacency neighborhoods and uses decoder $\text{DEC}(\textbf{z}_i,\textbf{z}_j) := \frac{e^{\textbf{z}_{i}^{T}\textbf{z}_j}}{\sum_{v_{k}\in\mathcal{V}}e^{\textbf{z}_{i}^{T}\textbf{z}_{k}}}$. Both the first-order and second-order objectives are optimized using loss functions derived from the KL-divergence metrics.

HARP: Extending random-walk embeddings via graph pre-processing: Collapse related nodes in $\mathcal{G}$ together into "supernodes". After embedding the coarsened version of $\mathcal{G}$, they then run DeepWalk, node2vec, or LINE on this coarsened graph with the supernode embedding being the initial value for the random walk embeddings of the supernode's constituent nodes.

The authors of HARP consider two kinds of graph coarsening methods: edge collapsing for preserving first-order proximity and star collapsing for preserving second-order proximity. First-order proximity is concerned with preserving the observed edges in the input graph while second-order proximity is based on the shared neighborhood structure of the nodes.

Edge collapsing selects $E'\subset E$ such that no two edges in $E'$ are incident to the same vertex. Then $\forall (u_i,v_i)\in E'$, it merges $(u_i,v_i)$ into a single node $w_i$, and merge the edges incident to $u_i$ and $v_i$. The number of nodes in the coarser graph is therefore at least half of that in the original graph. Star collapsing merges nodes with same neighbors. For each round of collapsing, the authors perform first star collapsing and then edge collapsing.

Additional variants of the random-walk idea: Walklets extend the DeepWalk algorithm to learn embeddings using random walks that "skip" or "hop" over multiple nodes at each step, resulting in a proximity measure similar to GraRep. Neural Embeddings of Graphs in Hyperbolic Space modify the inner-product decoder of node2vec to use a hyperbolic distance measure to replace the Euclidean distance measure.

Generalized Encoder-Decoder Architectures

The direct encoding approaches have several drawbacks:

• High space complexity $O(|\mathcal{V}|)$ due to a lack of parameter sharing

• No utilization of content and structral information of the graph

• Transductive and cannot generalize to unseen nodes

There have been many efforts in proposing new approaches

Neighborhood autoencoder methods

Deep Neural Graph Representations and Structural Deep Network Embeddings directly incorporate graph structure into the encoder algorithm. They use autoencoders to compress information about a node's local neighborhood and use a unary decoder.

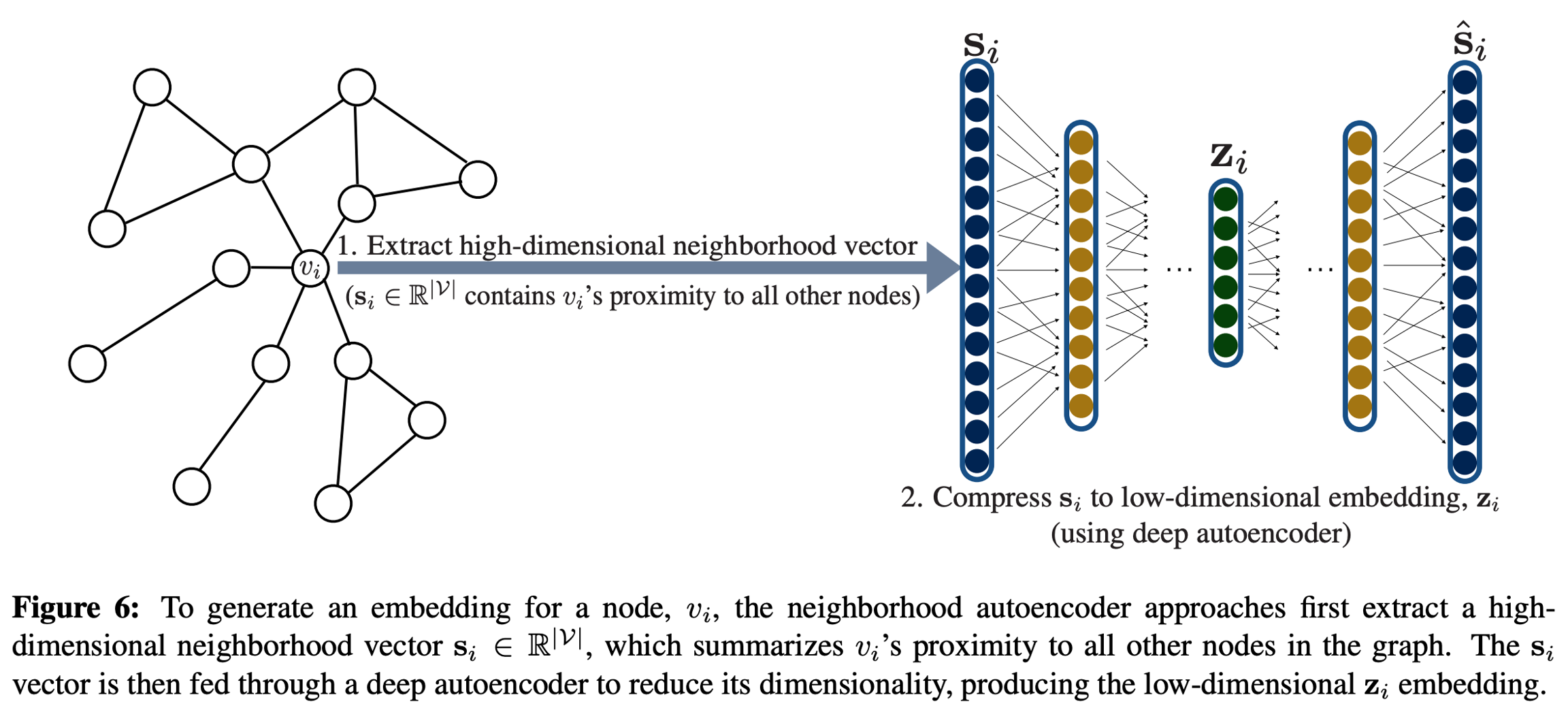
SDNE and DNGR differ in the similarity functions they use to construct the neighborhood vectors $s_i$ and optimization objectives. DNGR defines $s_i$ according to the pointwise mutual information of two nodes co-occuring on random walks, similar to DeepWalk and node2vec. SDNE simply sets $s_i:=A_i$, i.e. $v_i$'s row or column in adjacency matrix. SDNE also combines the reconstruction loss with the Laplacian eigenmaps objective $\sum_{(v_i,v_j)\in \mathcal{D}}\text{DEC}(\textbf{z}_i,\textbf{z}_j)s_{\mathcal{G}}(v_i,v_j)$.

The autoencoder based approach still has many limitations:

• $s_i$ is $O(|\mathcal{V}|)$

• It does not directly utilize proximity of higher orders

• It cannot handle graphs with variable size

Neighborhood Aggregation and Convolutional Encoders

This group of approaches generate node embeddings based on its local neighborhood sturcture and related node features. In cases where attribute data is not given, these methods can use simple graph statistics as attributes (e.g., node degrees) or assign each node a one-hot indicator vector as an attribute. These methods are often called convolutional because the local neighborhood concerned is similar to receptive field of ConvNet and they have theoretical connections to approximate spectral kernels on graphs.

Below is an example algorithm:

The difference between various algorithms is primarily in line $4$ and line $5$. In GraphSage for example, the authors used concatenation in line $5$ and tried 3 different aggregation in line $4$: elementwise mean, max pooling and LSTM. The best aggregator based on their experiment is max pooling. GCNs and column networks use a weighted sum in line $5$ and a weighted element-wise mean in line $4$.

Column networks also interpolate between the old features and the new features before line $7$: $\textbf{h}_{v}^{k'} = \alpha\textbf{h}_{v}^{k} + (1-\alpha)\textbf{h}_{v}^{k-1}$.

Note that in principle these neighborhood based encoders can be combined with any decoder and loss function that we mentioned before.

Incorporating task-specific supervision

Most approaches we mentioned above are doing unsupervised learning, but we can also incorporate task-specific supervision like node classification.

Extensions to multi-modal graphs

Dealing with different node and edge types

The general strategy is to use different encoders for nodes of different types and use edge type specific parameters in pairwise decoders. For example, the standard inner-product edge decoder can be replaced with a bilinear form:

$$\begin{equation} \textbf{z}^{T}\textbf{A}_{\tau}\textbf{z}, \end{equation}$$

where $\tau$ indexes edge type and $\textbf{A}_{\tau}$ is a learned parameter.

metapath2vec proposed a strategy for sampling random walks from the heterogeneous graphs, where the random walks are restricted to only transition between particular types of nodes.

Tying node embeddings across layers

Graphs can have multiple "layers" that contain copies of the same nodes like in the figure below:

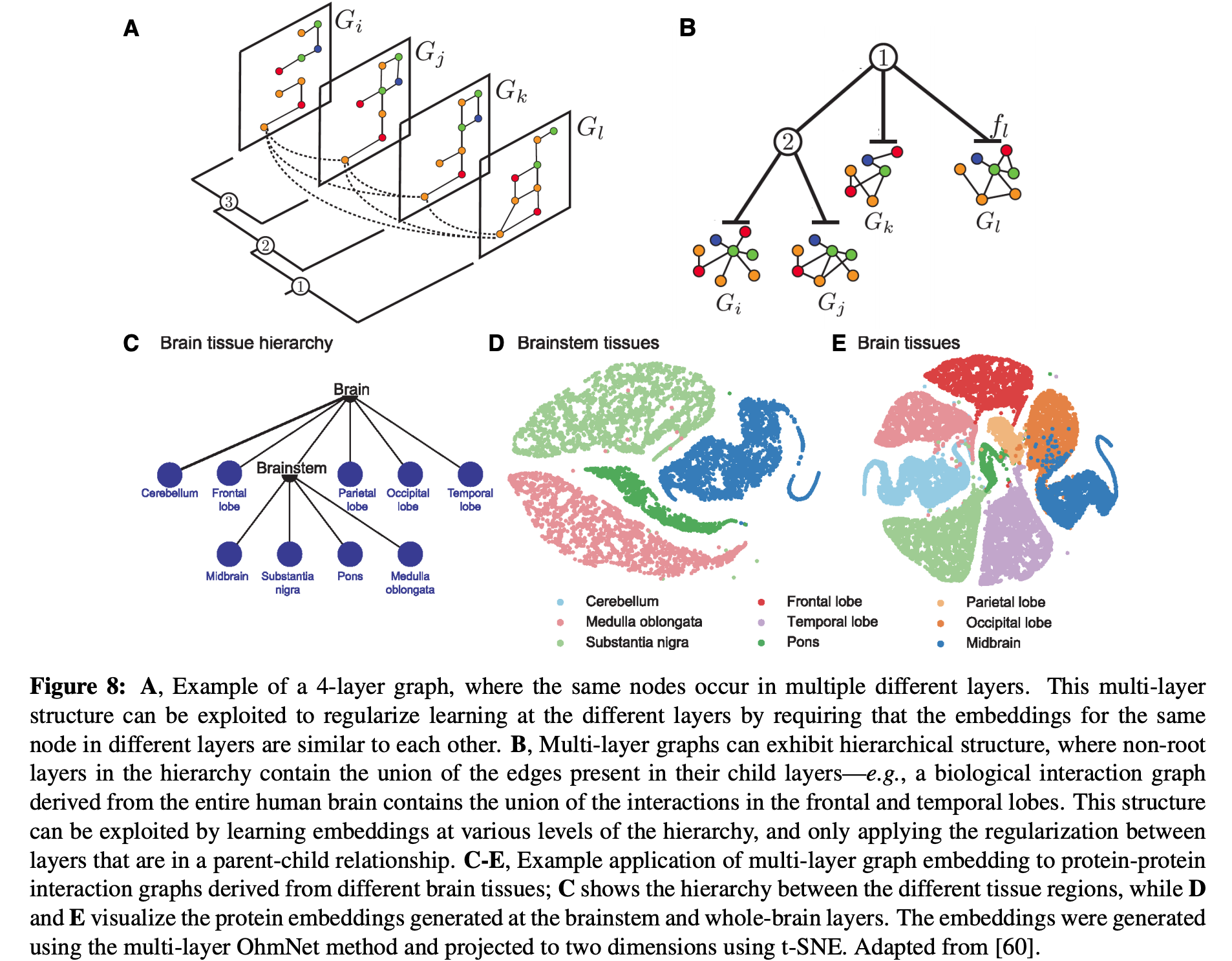
In these cases it can be beneficial to share information across layers. For example we can add a regularization to minimize the discrepancy between embeddings for a same node across layers.

Embedding Structural Roles

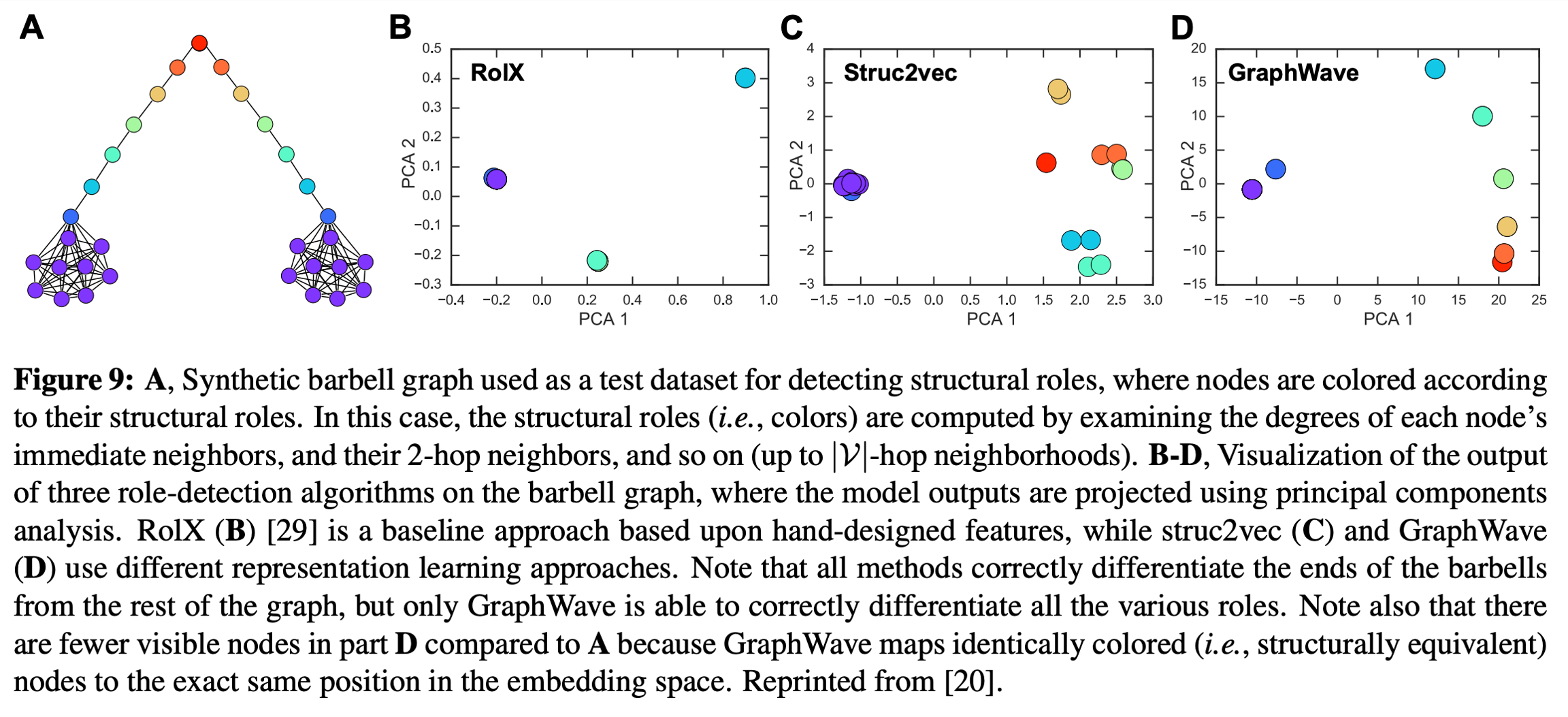
In many tasks it is more important to learn representations that correspond to the structural roles of the nodes, independent of their global graph positions. One possibility is to bias the random walks as in node2vec. More recently, struc2vec and GraphWave have developed node embedding approaches that are specifically designed to capture structural roles.

struc2vec generates a series of weighted auxiliary graphs $\mathcal{G}_{k}', k=1, 2, \cdots$, where $\mathcal{G}_{k}'$ captures structural similarities between nodes' $k$-hop neighborhoods. Let $R_{k}(v_i)$ denote the ordered sequence of degrees of the nodes that are exactly $k$-hops away from $v_i$, the edge weights $w_k(v_i,v_j)$ in $\mathcal{G}_{k}'$ are recursively defined as

$$\begin{equation} w_{k}(v_i,v_j) = w_{k-1}(v_i,v_j) + d(R_{k}(v_i), R_{k}(v_j)), \end{equation}$$

where $w_{0}(v_i, v_j)=0$ and $d(R_{k}(v_i), R_{k}(v_j))$ measures the "distance" between $R_{k}(v_i)$ and $R_{k}(v_j)$. Biased random walks can be performed based on $\mathcal{G}_{k}'$'s.

GraphWave relies on spectral graph wavelets and heat kernels. Let $L$ denote the unnormalized Laplacian, $U$ and $\lambda_i, i=1,\cdots,|\mathcal{V}|$ denote the eigenvectors and eigenvalues of $L$. Assume we have a heat kernel $g(\lambda)=e^{-s\lambda}$ with pre-defined scale $s$. GraphWave encodes the structure role of node $v_i$ by computing

$$\begin{equation} \psi_{v_i}=\textbf{U}\textbf{G}\textbf{U}^{T}\textbf{v}_i, \end{equation}$$

where $\textbf{G}=\text{diag}([g(\lambda_1),\cdots,g(\lambda_{|\mathcal{V}|})])$ and $\textbf{v}_i$ is a one-hot vector corresponding to $v_i$. The authors of GraphWave show that $\psi_{v_i}$'s implicitly relate to topological quantities, such as $v_i$'s degree and the number of $k$-cycles $v_i$ is involved in. They find that -- with a proper choice of $s$ -- GraphWave is able to effectively capture structural information about a node's role in a graph as in the below figure:

Subgraph Embeddings

We may want to encode a set of nodes and edges into a low-dimensional vector embedding. This is necessary for graph classification and has potential applications in classifying or predicting various properties of molecular graphs, predicting whether a program satisfies certain formal properties and performing logical reasoning tasks.

Representation learning on subgraphs is closely related to the design of graph kernels, which define a distance measure between subgraphs. The authors omit a detailed discussion of graph kernels and refer the readers to Graph Kernels. In the review, the authors mainly focus on data driven methods.

Sets of Node Embeddings and Convolutional Approaches

Many methods can be viewed as direct extensions of the convolutional node embedding algorithms where people aggregate node embeddings corresponding to subgraphs.

Sum-based Approaches

Let $S\subset\mathcal{V}$ be a collection of nodes forming a subgraph. The easiest subgraph embedding can be defined as

$$\begin{equation} \textbf{z}_{S}=\sum_{v_i\in S}\textbf{z}_i \end{equation}$$

One can also incorporate edge embeddings.

Graph-coarsening approaches

One can also repeatedly cluster the nodes and apply an elementwise maximum over the node embeddings to get cluster embeddings.

Further Variants

Molecular Graph Convolutions: Moving Beyond Fingerprints aggregate sets of nodes using "fuzzy" histograms instead of a sum. I find this to be similar to a soft cluster assignment. Neipart et al. use a domain specific method for sorting the nodes and concatenate node features according to the order. The concatenated node features is then fed through a ConvNet.

Graph Neural Networks (GNNs)

Instead of aggregating information from neighbors, the intuition behind GNNs is that subgraphs can be viewed as specifying a "compute graph", i.e., a recipe for accumulating and passing information between nodes.

In the original GNN, every node feature is initialized with a random embedding $\textbf{h}_{i}^{0}$ and at each iteration the features for all nodes are updated with

$$\begin{equation} \textbf{h}_{i}^{k} = \sum_{v_j\in\mathcal{N}(v_i)}\sigma(\textbf{W}\textbf{h}_{j}^{k-1}+\textbf{b}), \end{equation}$$

where $\textbf{W}\in\mathbb{R}^{d\times d}$ and $\textbf{b}\in\mathbb{R}^{d}$ are trainable parameters and $\sigma$ is a non-linearity (e.g., $\text{tanh}$ or a $\text{ReLU}$). Special care must be taken during initialization to ensure convergence of node features. We can then aggregate node features for subgraphs using methods we mentioned before.

Gated Graph Neural Networks extend GNN with GRU and BP through time. This development removes the need for node embeddings to converge, allows to leverage node attributes and use the output of intermediate embeddings of subgraphs.

The GNN framework is highly expressive but also computationally expensive. Comparing to the convolutional approaches, which are most commonly used to classify molecular graphs in large datasets, the GNN approach has been used for more complex, but smaller scale tasks, e.g., approximate formal verification using graph-based representations of programs.

Future Directions

Scalability: Scale node and graph embedding to billions of nodes and edges.

Decoding higher-order motifs: Most methods rely on basic pairwise decoders, which predict pairwise relations between nodes and ignore higher-order graph structures involving more than two nodes. Decoding algorithms that are capable of decoding complex motifs is an important direction for future work.

Modeling dynamic, temporal graphs

Reasoning about large sets of candidate subgraphs: Discover subgraphs with certain properties.

Improving interpretability