GraphSAGE

tags: graph-networks, nips-2017

GraphSAGE

Difference with previous works

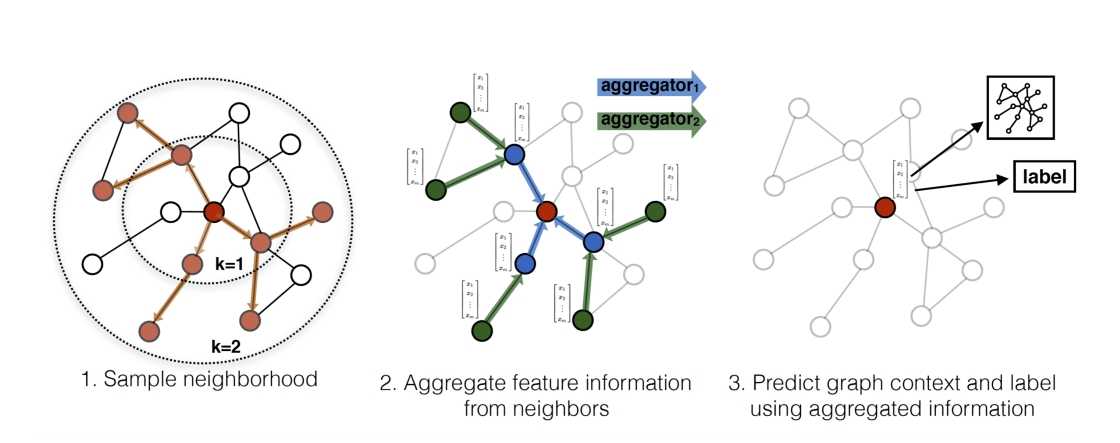
• Instead of training individual embeddings for each node, GraphSAGE learn a function that generates embeddings by sampling and aggregating features from a node's local neighborhood.

• Inductive setting:

  • Previous work focused on embeddings nodes from a single fixed graph.

  • Real-world application requires embeddings to be quickly generated

    for unseen words or entirely new graphs.

  • operate on evolving graphs and constantly encounter unseen nodes.

Difficulty of Inductive Learning

• Generalize to unseen nodes requires "aligning" newly observed subgraphs to node embeddings that the algorithm has already optimized on. - An inductive framework must learn to recognize structural properties of a node's neighborhood that reveal the node's local role in the graph and its global position.

img

Related Works

• Factorization-based embedding approaches.

• Supervised Learning over graphs.

  • Kernel-based approaches.

• Graph convolutional networks.

Algorithm

img

Forward Propagation

The forward propagation assumes that the model has already been trained and that the parameters are fixed.

Assume that we have learned the parameters of $K$ aggregator functions, which aggregate information from node neighbors, as well as a set of weight matrices $\mathbf{W}^k$.

The final representations output at depth $K$ is

$$\mathbf { z } _ { v } \equiv \mathbf { h } _ { v } ^ { K } , \forall v \in \mathcal { V }$$

Neighborhood

Instead of using full neighborhood set, they uniformly sample a fixed-size set of neighbors:

$$\mathcal{N}(v) = \{u\in \mathcal{V}: (u, v)\in \mathcal{E} \}$$

in order to keep the computational footprint of each batch fixed. Per-batch space and time complexity for GraphSAGE is $O(\prod_{i=1}^{K}S_i)$.

Practical setting: $K=2$, $S_1 \cdot S_2 \leq 500$.

Aggregators

Mean aggregator

$$\operatorname { AGGREGATE } _ {k} ^ {\mathrm {mean}} = \sum_{u\in \mathcal{N}(v)}\frac{\mathbf{h}_u^{k-1}}{|\mathcal{N}(v)|}$$

Convolutional aggregator

$$\mathbf { h } _ { v } ^ { k } \leftarrow \sigma \left( \mathbf { W } \cdot \operatorname { MEAN } \left( \left\{ \mathbf { h } _ { v } ^ { k - 1 } \right\} \cup \left\{ \mathbf { h } _ { u } ^ { k - 1 } , \forall u \in \mathcal { N } ( v ) \right\} \right)\right.$$

• Compared to mean aggregator, the convolutional aggregator does not perform the concatenation operation in line 5 of the algorithm, which could be viewed as a skip-connection.

LSTM aggregator

• Larger expressive capability.

• Not inherently symmetric(not permutation invariant)

• They adapt LSTMs to operate on an unordered set by simply applying the LSTMs to a random permutation of the node's neighbors.

Pooling aggregator

$$\operatorname { AGGREGATE } _ { k } ^ { \mathrm { pool } } = \max \left( \left\{ \sigma \left( \mathbf { W } _ { \mathrm { pool } } \mathbf { h } _ { u _ { i } } ^ { k } + \mathbf { b } \right) , \forall u _ { i } \in \mathcal { N } ( v ) \right\} \right)$$

Loss (In Unsupervised Setting)

The loss function encourages nearby nodes to have similar representations, while enforcing that the representations of disparate nodes are highly distinct.

$$J _ { \mathcal { G } } \left( \mathbf { z } _ { u } \right) = - \log \left( \sigma \left( \mathbf { z } _ { u } ^ { \top } \mathbf { z } _ { v } \right) \right) - Q \cdot \mathbb { E } _ { v _ { n } \sim P _ { n } ( v ) } \log \left( \sigma \left( - \mathbf { z } _ { u } ^ { \top } \mathbf { z } _ { v _ { n } } \right) \right)$$

$v$ is a node that co-occurs near $u$ on a fixed-length random walk. $Q$ defines the number of negative samples.

Unlike previous embedding approaches, no "context embedding" is required.

Relation to Weisfeiler-Lehman Isomorphism Test

The Weisfeiler-Lehman algorithm and estimation on graphs

It's trivial to test whether two graphs are isomorphism if all vertices have unique attributes.

The idea of WL test is to assign fingerprints to vertices and their neighborhoods repeatedly. To start with, we assign each node with attribute $1$:

1. Compute a hash of $\left( a _ { v } , a _ { v _ { 1 } } , \dots , a _ { v _ { n } } \right)$ where $v_i$ are neighbors of vertex $v$.
2. Use the hash as attribute for next iteration.

Note that the WL test fails when the graph has some kind of symmetry: if $u$ and $v$ are symmetric in the graph, WL test would assign they with the same attribute.

WL test in GraphSAGE

The isomorphism test could be viewed as applying a simplified GraphSAGE on graphs:

1. Set $K = | \mathcal { V } |$
2. Set the weight matrices as the identity.

3. Use hash function as the aggregator.

Experiments

1. Classifying academic papers into different subjects using WOS citation dataset.

2. Classifying reddit posts as belonging to different communities.

3. Classifying protein functions across various biological PPI graphs.

Unsupervised Setting

For unsupervised objective, GraphSAGE ran $50$ random walks of length $5$ for each node in order to obtain the pairs needed for negative sampling.

To make predictions on the embeddings output from the unsupervised models, GraphSAGE use logistic SGD Classifier.

Inductive learning on evolving graphs

• Citation

  • The authors train all algorithms on 2000-2004 data and use 2005 data for testing.

  • Label: 6 different field labels.

  • Features: node degrees, sentence embedding.

• Reddit

  • First 20 days for training and others for testing.

  • Label: community(subreddit)

  • Features: Concatenation of average embedding of post title, average embedding of post's comments, post's score & number of comments.

Generalizing across graphs: PPI

In this experiment the authors conduct experiments on protein-protein interactions, this requires learning about node roles rather then community structure.

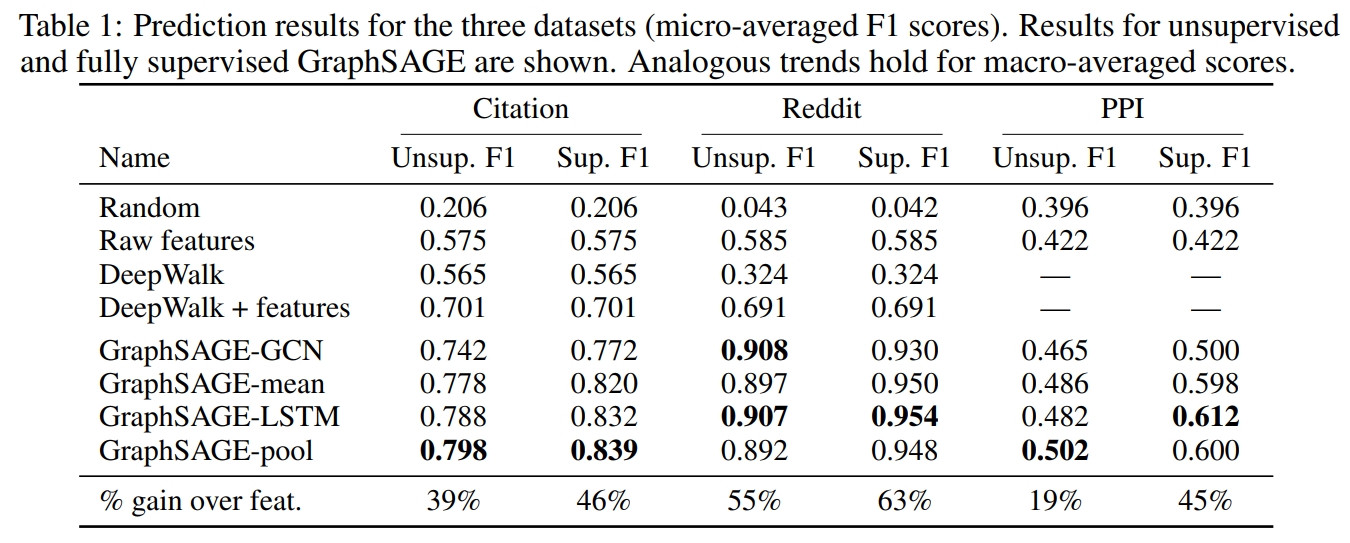
Results

img